应用场景
队列是遵循先进先出(First-In-First-Out)模式的,但有时需要在队列中基于优先级处理对象。 举个例子:作业系统中的调度程序,当一个作业完成后,需要在所有等待调度的作业中选择一个优先级最高的作业来执行,并且也可以添加一个新的作业到作业的优先队列中。
优先队列,也就是队列里面的元素遵从一定的比较规则(比较器比较)有序。比如DelayQueue底层用到PriorityQueue实现,也就是PriorityQueue里面保存的元素是按照超过过期时间由小到大排序的有序队列。
PriorityQueue不允许空值,而且不支持non-comparable(不可比较)的对象,比如用户自定义的类。优先队列要求使用Java Comparable和Comparator接口给对象排序,并且在排序时会按照优先级处理其中的元素。
类继承图
优先队列的类继承关系相对简单,主要是主要是实现了两个接口:Collection和Queue,类继承图如下: 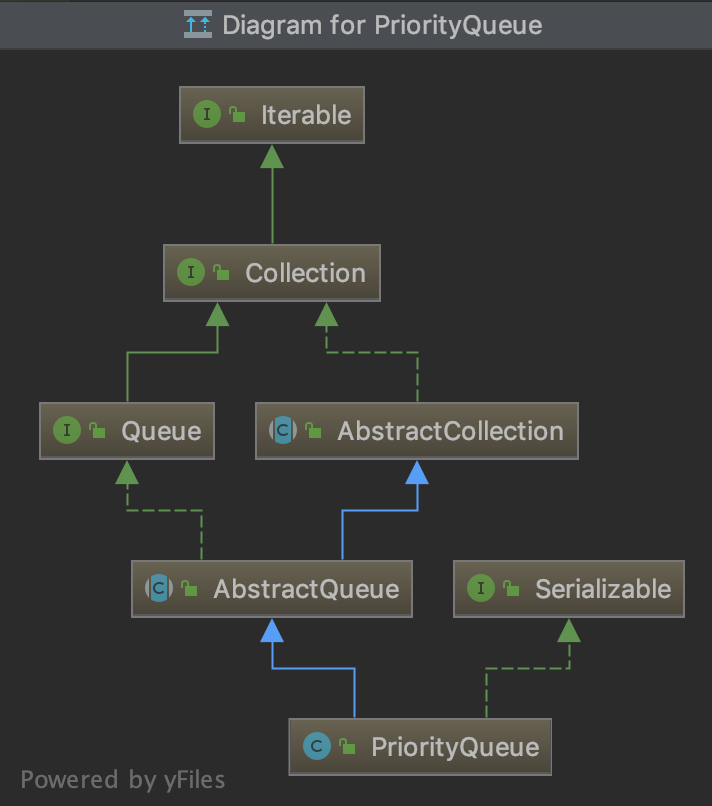 PS: IDEA中,在指定类右键查看diagram 也可以使用快捷键command+alt+u。
PS: IDEA中,在指定类右键查看diagram 也可以使用快捷键command+alt+u。
底层数据结构
首先看下PriorityQueue的核心成员属性
1
2
3
4
transient Object[] queue;// 队列使用数组保存数据
private int size = 0;//队列的大小
/** 队列里面的元素使用的比较器,如果不指定,就是用元素自己默认的比较器。PriorityQueue就是通过这个比较器来实现排序 */
private final Comparator<? super E> comparator;
可以看出PriorityQueue是使用最小堆实现的优先队列的存储。 它是使用数组保存数据,用Comparator比较器实现有序的。
下面以一张图来解释存储结构: 以一个优先队列:3、5、7、9、10、11、12、13、15、20. 为例,以下是存储结构 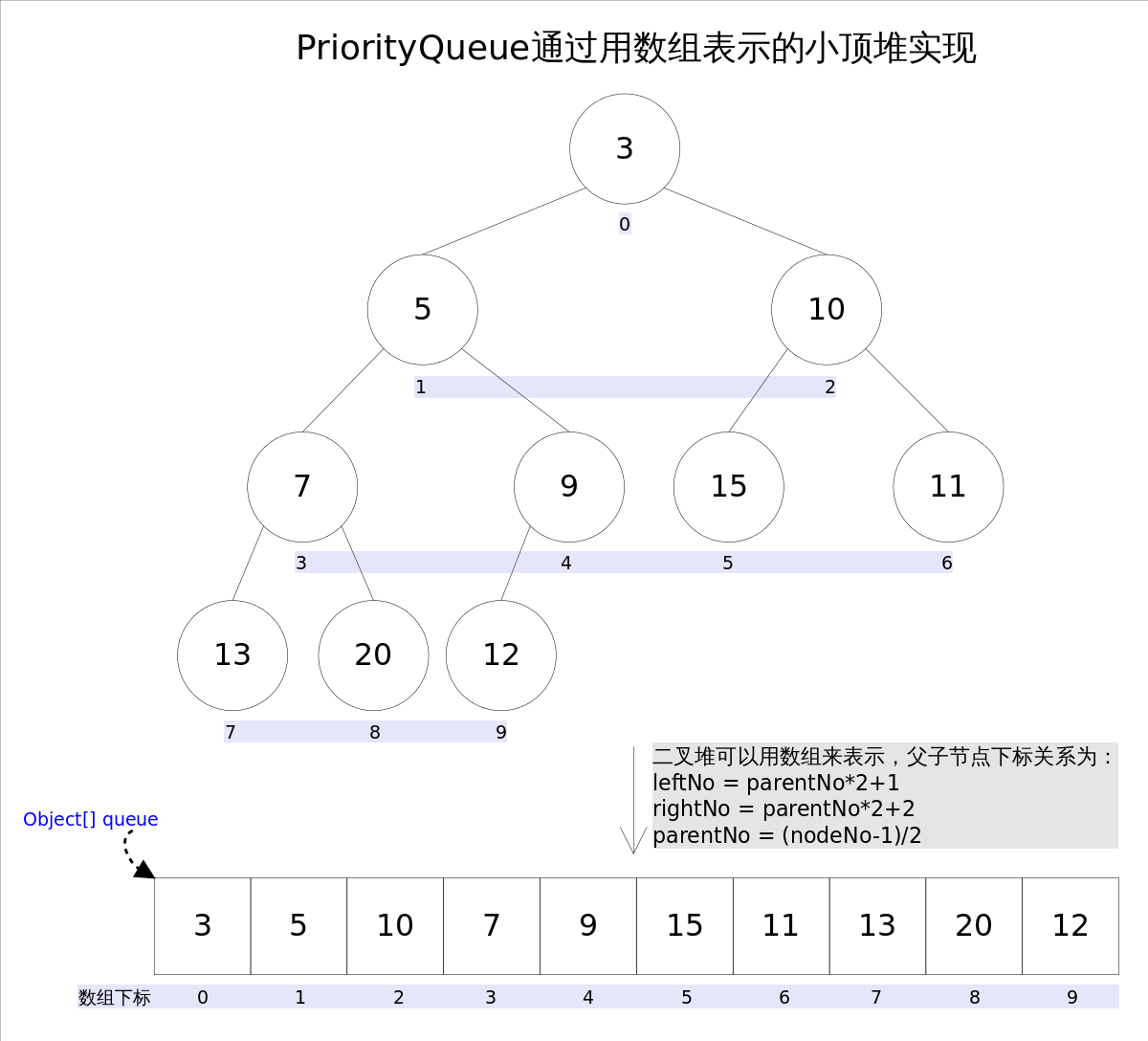 上图中我们给每个元素按照层序遍历的方式进行了编号,如果你足够细心,会发现父节点和子节点的编号是有联系的,更确切的说父子节点的编号之间有如下关系:
上图中我们给每个元素按照层序遍历的方式进行了编号,如果你足够细心,会发现父节点和子节点的编号是有联系的,更确切的说父子节点的编号之间有如下关系:
1
2
3
4
5
leftNo = parentNo*2+1
rightNo = parentNo*2+2
parentNo = (nodeNo-1)/2
通过上述三个公式,可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。
PriorityQueue的peek()和element操作是常数时间,add(), offer(), 无参数的remove()以及poll()方法的时间复杂度都是log(N)。 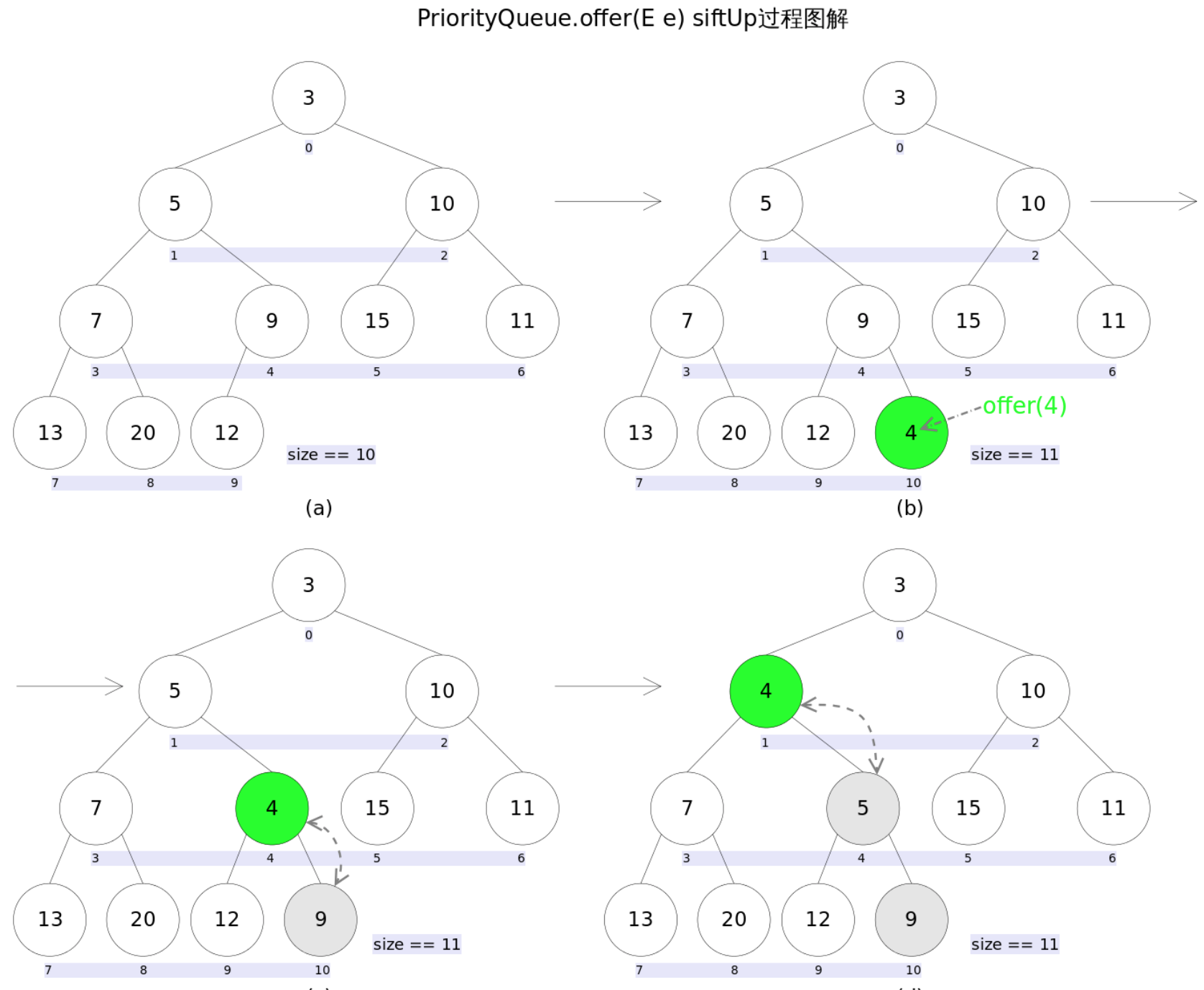
add() 和 offer()
这里add(E e)和offer(E e)的语义相同,都是向优先队列中插入元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public boolean offer(E e) {
if (e == null) //禁止放入空元素
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1); //自动扩容,申请一个更大的数组
size = i + 1;
if (i == 0) //原队列为空,插入第一个元素
queue[0] = e;
else
siftUp(i, e); //调整堆结构
return true;
}
新加入的元素x可能会破坏小顶堆的性质,因此需要进行调整。调整的过程为:从k指定的位置开始,将x逐层与当前点的parent进行比较并交换,直到满足x >= queue[parent]为止。注意这里的比较可以是元素的自然顺序,也可以是依靠比较器的顺序。
peek()
返回优先级队列的最小的元素,由于PriorityQueue底层基于最小堆,最小堆又采用数组存储,所以堆顶元素即数组的第一个元素。
1
2
3
public E peek() {
return (size == 0) ? null : (E) queue[0];
}
remove()和poll()
remove()和poll()方法的语义也完全相同,都是获取并删除队首元素,区别是当方法失败时前者抛出异常,后者返回null。由于删除操作会改变队列的结构,为维护小顶堆的性质,需要进行必要的调整。
下图以删除最小元素3 为例: 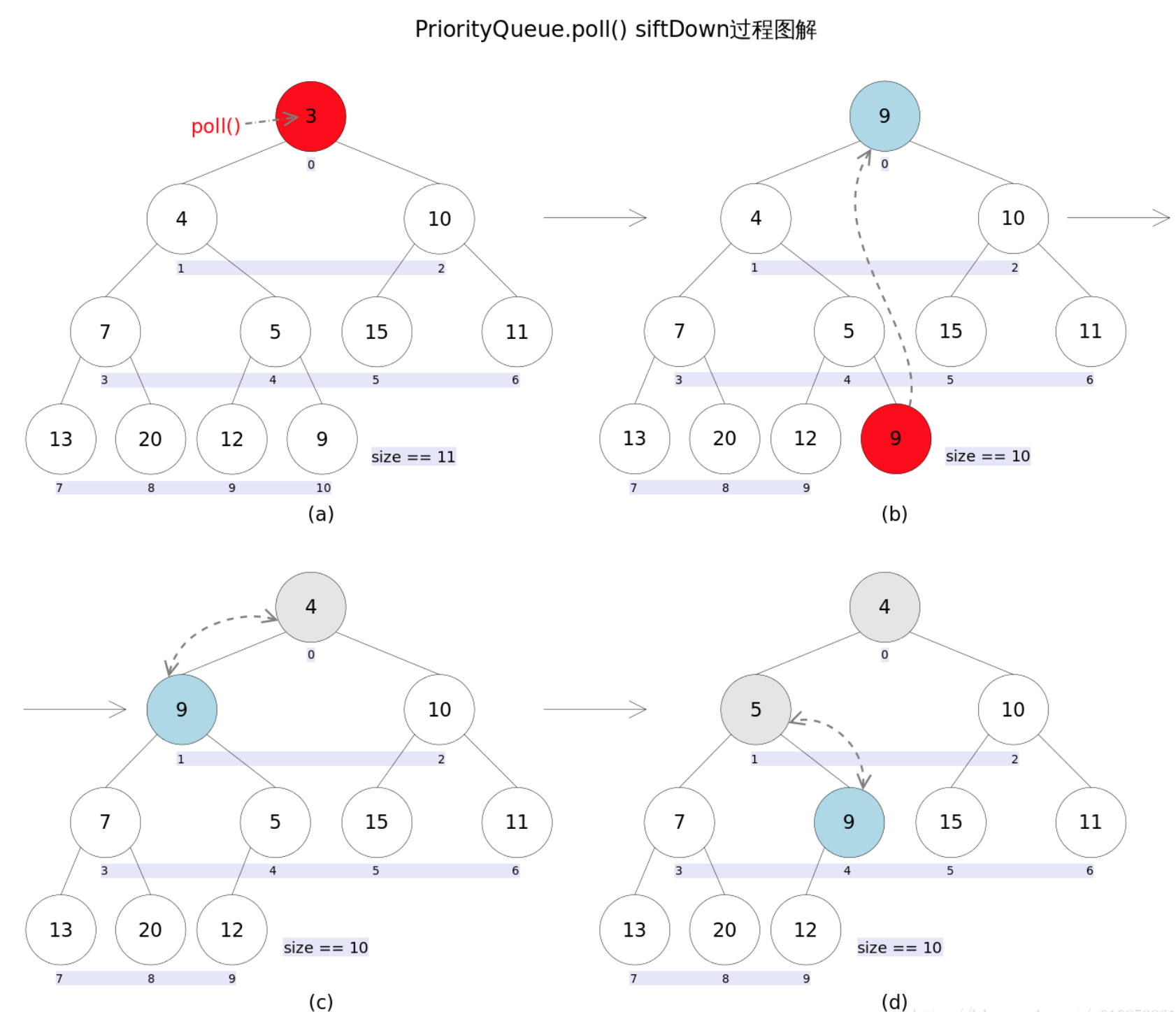 下面是源码:
下面是源码:
1
2
3
4
5
6
7
8
9
10
11
12
public E poll() {
if (size == 0)
return null;
int s = --size;
modCount++;
E result = (E) queue[0];
E x = (E) queue[s];
queue[s] = null;
if (s != 0)
siftDown(0, x);
return result;
}
上述代码首先记录0下标处的元素,并用最后一个元素替换0下标位置的元素,之后调用siftDown()方法对堆进行调整,最后返回原来0下标处的那个元素(也就是最小的那个元素)。重点是siftDown(int k, E x)方法,siftDown()会直接调用siftDownComparable()方法,该方法的作用是从k指定的位置开始,将x逐层向下与当前点的左右孩子中较小的那个交换,直到x小于或等于左右孩子中的任何一个为止。